Logical Entailment
every interpretation that satisfies the premises also satisfies the
conclusion.
Herbrand Summary
Herbrand Method works for Basic Logic and Universal Logic,
but there can be many interpretations.
Herbrand Method does not work for Existential Logic.
Herbrand Method works for Functional Logic, but infinitely
many interpretations
Solution: Use formal proof s!
Formal Proofs
A formal proof of ϕ from Δ is a sequence of sentences
terminating in ϕ in which each item is either:
1. a premise (a member of Δ)
2. an instance of an axiom schema
3. the result of applying a rule of inf erence to earlier items
in the sequence.
Old Rules of Inference
Idea for Universal Instantiation
Warning: This is not quite right.
Examples
Inappropriateness
A term τ is inappropriate for a variable ν in ϕ if and only if τ
contains a variable μ and there is some free occurrence of ν in
ϕ that lies in the scope of a quantif ier of μ.
mother(x) is inappropriate for y in ∃x.hates(x,y).
Substitutability
A term τ is substitutable for ν in ϕ if and only if it is not
inappropriate with ν in ϕ.
Some texts say “x is free for y in ϕ” instead of “x is
substitutable for y in ϕ”.
Universal Instantiation
Existential Instantiation I
Examples
Existential Instantiation II
Examples
Formal Proofs
A formal proof of ϕ from Δ is a sequence of sentences
terminating in ϕ in which each item is either:
1. a premise (a member of Δ)
2. an instance of an axiom schema
3. the result of applying a rule of inf erence to earlier items
in the sequence.
Example
Everybody loves somebody. Everybody loves a lover. Show
that Jack loves Jill.
Standard Axiom Schemata
Standard Axiom Schemata (continued)
Provability
A sentence ϕ is provable from a set of sentences Δ if and only
if there is a finite formal proof of ϕ from Δ using only Modus
Ponens and the standard axiom schemata.
Soundness Theorem: If ϕ is provable from Δ, then Δ logically
entails ϕ.
Completeness Theorem (Godel): If Δ logically entails ϕ, then ϕ
is provable from Δ.
Decidability
A class of questions is decidable if and only if there is a
procedure such that, when given as input any question in the
class, the procedure halts and says yes if the answer is positive
and no if the answer is negative.
Example: For any natural number n, determining whether n is
prime.
Semidecidability
A class of questions is semidecidable if and only if there is a
procedure that halts and says yes if the answer is positive.
Obvious Fact: If a class of questions is decidable, it is
semidecidable.
Semidecidability of Logical Entailment
Decidability Not Proved
Note that we have not shown that logical entailment for
Relational Logic is decidable.
The procedure may not halt.
p(x) ⇒p(f(x))
p(f(f(a)))
p(f(b))?
Wecannot just run procedure on negated sentence because that
may not be logically implied either!
p(x) ⇒p(f(x))
p(f(f(a)))
¬p(f(b))?
Undecidability of Logical Entailment
Metatheorem: Logical Entailment f or Relational Logic is not
decidable.
Proof: Suppose there is a procedure p that decides the question
of logical entailment. Its inputs are Δ and ϕ.
Wecan encode the behavior of a machine and its inputs as
sentences and ask whether the machine halts as a conclusion.
What happens if we give this description and question to p? It
says yes.
Undecidability (continued)
It is possible to construct a larger machine p’ that enters an
inf inite loop if p says yes and halts if p says no.
Wecan encode a description of this machine as a set of
sentences and ask whether the machine halts as a conclusion.
What happens if we give this description and question to p? If
p says yes, then p’ runs f orever, contradicting the hypothesis
that p computes correctly. If p says no, then p’ halts, once
again contradicting answer from p. QED.
Closure
The closure S* of a set S of sentences is the set of all
sentences logically entailed by S.
Theories
A theory is a set of sentences closed under logical entailment,
i.e. T is a theory if and only if T*=T.
A theory T is finitely axiomatizable if and only if there is a
finite set Δ of sentences such that T=Δ*.
A theory T is complete if and only, f or all ϕ, either ϕ∈T or
¬ϕ∈T.
Note: Not every theory is complete. Consider the theory
consisting of all consequences of p(a,b). Does this include
p(b,a)? Does it include ¬p(b,a)?
Arithmetization of Logical Entailment
The theory of arithmetic is the set of all sentences true of the
natural numbers, 0, 1, + , *, and <.
Fact: It is possible to assign numbers to sentences such that
(1) Every sentence ϕ is assigned a unique number nϕ.
(2) The question of logical entailment Δ|=ϕ can be expressed
as a numerical condition r(nΔ,nϕ).
Conclusion: The theory of arithmetic is not decidable.
Incompleteness Theorem
Metatheorem (Godel): If Δ is a finite subset of the theory of
arithmetic, then Δ* is not complete.
Variant: Arithmetic is not finitely axiomatizable.
Proof: If there were a finite axiomatization, then the theory
would be decidable. However, arithmetic is not decidable.
Therefore, there is no finite axiomatization.
Summary
Logical Entailment for Relational Logic is semidecidable.
Logical Entailment for Relational Logic is not decidable.
Arithmetic is not finitely axiomatizable in Relational Logic.
This is dummy text. It is not meant to be read. Accordingly, it is difficult to figure out when to end it. But then, this is dummy text. It is not meant to be read. Period.
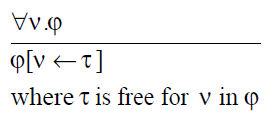
ConversionConversion EmoticonEmoticon